Dans cet article nous allons explorer l’ensemble de Mandelbrot. Le but ici est de se familiariser avec le développement C tout en mettant en place une version initiale d’un calcul relativement intensif. L’exemple retenu ici est le dessin de l’ensemble de Mandelbrot en reposant sur la petite bibliothèque de dessin PPM que nous avons précédement introduite. Ensuite, une fois le problème initial définit et une première implémentation réalisée, nous profilerons le programme pour identifier de potentielles optimisations. Enfin nous réaliserons une étude de scalabilité sur architecture KNL pour illustrer les métriques de performance HPC de base.
L’ensemble de Mandelbrot
Benoit Mandelbrot, de nationalité Française présente la notion de rugosité dans la vidéo ci-dessus. Nous allons ici nous intérésser à la fractale qui porte son nom. Cet objet de curiosité est d’une infinie complexité bien que commes nous allons voir naissant d’une simple formule répétée infiniment. Où comme le dit Mr. Mandelbrot à la fin de la vidéo ci-dessus: « Des merveilles insondables naissent de règles simples.. répétée indéfiniment ».
Ici nous allons tout d’abord définir la méthode pour générer cet ensemble qui est défini dans le plan complexe. On note Z un nombre complexe et ^2 le carré de ce nombre. Enfin on définit |Z| comme le module d’un nombre complexe.
L’ensemble de Mandelbrot est défini de manière récursive pour tout point du plan complexe c comme suit:
Z(0) = 0
Z(n+1) = Z(n)^2 + c
L’ensemble de Mandelbrot M est tel que cette suite est bornée. Attachons nous maintenant à définir en termes informatiques cette abstraction mathématique.
Les Complexes en C
On l’oublie parfois mais le C propose en standard des fonction et un support des nombres complexes. Pour le vérifier vous pouvez consulter le manuel associé:
man complex
Mandelbrot en C
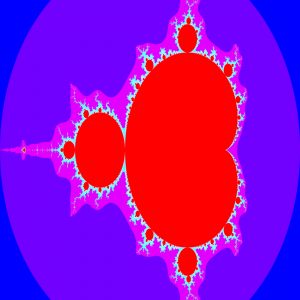
Nous allons donc utiliser ces nombres directement, évitant ainsi de réinventer des complexes et de nous tromper dans les calculs de modules et de produits. Représentons nous maintenant l’ensemble de Mandelbrot:
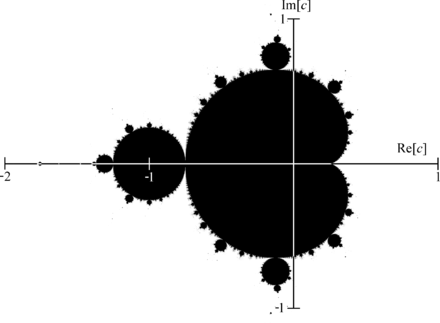
SOURCE ARTICLE WIKIPEDIA (domaine public)
On voit ici qu’il est présent dans le plan complexe entre -2 et 1 sur l’axe des réels et entre -1 et 1 sur l’axe des immaginaires. Dans une approche informatiques nous allons bien sûr devoir discrétiser cet espace pour y opérer les calculs, la mémoire de nos machines étant limitée. La première tâche est donc d’associer l’espace de définition de M à un tableau 2D de nombre complexes C, indexés de 0 à N.
Pour ce faire, il faut réaliser des fonction donnant pour un point du tableau ses coordonnées complexes telles qu’elle couvrent de manière uniforme l’espace cible. Cela revient à diviser uniformément, largeur et hauteur par le nombre de cases dans chaque dimension pour définir un pas q correspondant à la « largeur » d’une case.
On peut donc définir notre plan complexe comme suit:
#include <complex.h>
#define SIZEX 5000
#define SIZEY 5000
double cx( int x )
{
/* -2 ---> 1 */
static const double qx = 3.0 / (double)SIZEX;
return -2.0 + x * qx;
}
double cy( int y )
{
/* -1 ---> 1 */
static const double qy = 2.0 / (double)SIZEY;
return -1.0 + y * qy;
}
En utilisant ces deux fonctions il est alors possible de faire correspondre chaque case du tableau à un point du plan complexe. Nous allons maintenant écrire le calcul des points dans l’ensemble de Mandelbrot. Pour rappel ils sont définis par la fonctions récursive ci dessus sachant de plus que le module de la suite doit être inférieur à 2.0 pour ne pas diverger, donnant un point d’arrêt plus pratique à la récursivité. De plus, l’ensemble est généralement coloré en fonction du nombre d’itération avant d’atteindre cette limite de module. Enfin, afin de ne pas ittérer infiniment sur certains points, une limite d’ittérations est fixées, limitant le nombre d’invocation indiféramment du module. On obtient donc pour un point du plan complexe aux coordonnées (x,y) du tableau le calcul suivant:
#define TRSH 2.0
#define ITER 150ull
unsigned long int iter = 0;
double complex c = cx(x) + cy(y) * I;
double complex z = 0;
while(iter < ITER)
{
double mod = cabs(z);
if( TRSH < mod )
{
break;
}
z = z*z + c;
iter++;
}
color[x][y] = iter;
En appliquant maintenant cette formule à l’ensemble des points du plan complexe échantillonés par SIZEX et SIZEY, nous pouvons maintenant dessiner l’ensemble de Mandelbrot.
Le Code Initial
Ce premier dessin repose sur le code suivant en utilisant la bibliothèque de dessin PPM que nous avons précédement implémentée.
#include <stdio.h>
#include <complex.h>
#include <math.h>
#include "ppm.h"
#define TRSH 2.0
#define ITER 1024ull
#define SIZEX 1500
#define SIZEY 1500
double cx( int x )
{
/* -2 ---> 1 */
static const double qx = 3.0 / (double)SIZEX;
return -2.0 + x * qx;
}
double cy( int y )
{
/* -1 ---> 1 */
static const double qy = 2.0 / (double)SIZEY;
return -1.0 + y * qy;
}
int main(int argc, char *argv[])
{
struct ppm_image im;
ppm_image_init( &im , SIZEX , SIZEY );
int i,j;
double colref = 255.0/log(ITER);
for (i = 0; i < SIZEX; ++i) {
for (j = 0; j < SIZEY; ++j) {
unsigned long int iter = 0;
double complex c = cx(i) + cy(j) * I;
double complex z = 0;
while(iter < ITER)
{
double mod = cabs(z);
if( TRSH < mod )
{
break;
}
z = z*z + c;
iter++;
}
int grey = colref*log(iter);
ppm_image_setpixel(&im, i,j, grey, grey , grey );
}
}
ppm_image_dump( &im, "m.ppm");
ppm_image_release( &im );
return 0;
}
Dans ce code finalement très simple, on crée une image PPM aux dimensions SIZEX et SIZEY. Ensuite on parcours le plan complexe et on calcule « c » les coordonnées du point d’origine. Puis, on applique la récursivité tant que le module est inférieur à 2.0 et que le nombre limite d’itération n’est pas dépassé. Enfin, pour chaque point du plan retenu, on définit une couleur en niveau de gris dans l’image PPM. Notez que pour des raisons de lisibilité la valeur source subit un LOG
Un peu de couleur
Cette visualisation est un peu terne, elle ne tire pas avantage des trois canaux de notre image PPM couleur, le rendu étant fait en niveaux de gris. Nous alons maintenant parcourir le cube RGB (voir sur Wikimedia) pour apporter plus de dynamique à notre rendu. Le principe est relativement simple, il consiste à plaquer la dynamique de niveau de gris (normalisée entre 0 et 1 sur un nombre flotant) sur un parcours dans le cube RGB. On propose le code suivant (il est possible de tester avec une échelle linéaire):
struct col
{
int r;
int g;
int b;
};
struct col getcol( int val , int max )
{
double q = (double)val/(double)max;
struct col c = { 0, 0, 0 };
if( q < 0.25 )
{
c.r = ( q * 4.0 ) * 255.0;
c.b = 255;
}
else if( q < 0.5 )
{
c.b = 255;
c.g = 255;
c.r = (q-0.25)*4.0*255.0;
}
else if( q < 0.75 )
{
c.b = 255;
c.r = 255;
c.g = 255.0 - (q-0.5)*4.0*255.0;
}
else
{
c.b = 255-(q-0.75)*4.0*255.0;
c.g = 0;
c.r = 255;
}
return c;
}
Et on remplace le calcul de couleur:
double colref = log(ITER); //... struct col cc = getcol( log(iter), colref ); ppm_image_setpixel(&im, i,j, cc.r, cc.g , cc.b );
Ce qui donne le résultat suivant un peu plus coloré:
Performances Séquentielles
TODO
Parallélisation OpenMP
TODO